Aula Virtual CBTis92: GEOMETRÍA Y TRIGONOMETRÍA.- TRIÁNGULOS (SEMANA 5)

Triángulos clasificación y propiedades

¿Qué es un triángulo?

Un triángulo es un polígono de tres lados. La notación que se utiliza habitualmente es nombrar a sus vértices con las letras mayúsculas A, B y C (pero pueden ser otras, siempre que sean mayúsculas) y a los lados opuestos a estos vértices, con las respectivas minúsculas, tal como se observa en la imagen de portada.

¿Cuáles son sus propiedades más importantes?

Sus tres propiedades fundamentales son:

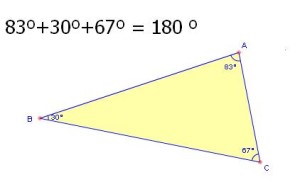
1) La suma de sus ángulos interiores es 180º.

Un ejemplo es el triángulo de la siguiente figura, donde consta la suma mencionada y su resultado:

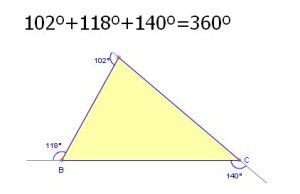
2) La suma de sus ángulos exteriores es 360º. Observa la siguiente figura como ejemplo de esta propiedad:

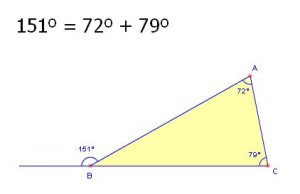
3) Cada ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes a él (o sea sus opuestos). Queda más claro en la siguiente figura que sirve como ejemplo:

¿Cómo se clasifican los triángulos?

Los triángulos se clasifican tradicionalmente en base a dos criterios, que pueden utilizarse juntos o separados. Veamos de qué se trata cada uno de ellos

==> Clasificación de triángulos según sus lados

Un triángulo es equilátero, si tiene sus tres lados iguales.
Un triángulo es isósceles, si tiene dos de sus lados iguales.
Un triángulo es escalenos, si tiene sus tres lados desiguales.

La siguiente imagen nos muestra con claridad uno de cada uno de estos tipos de triángulos, observa con cuidado:

clasificacion triángulos segun sus lados

==> Clasificación de triángulos según sus ángulos

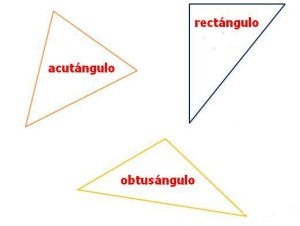
En este caso, nos fijamos en los ángulos para realizar la clasificación. A saber:

Un triángulo es acutángulo, si tiene todos sus ángulos agudos.
Un triángulo es rectángulos, si tiene uno de sus ángulos recto, vale decir de 90º.
Un triángulo es obtusángulo, si tiene un ángulo obtuso.

Veamos la siguiente figura para observar bien esta clasificación:

¿Cómo se calcula el perímetro de un triángulo?

Al igual que el perímetro de cualquier otro polígono, se calcula el perímetro de un triángulo simplemente sumando sus lados.

¿Cómo se calcula el área de un triángulo?

Como en casi todos los casos, tenemos una fórmula matemática que nos permite hallar el área o la superficie de un triángulo, cualquiera sea él, en relación a todas las categorías que vimos antes. En todos los casos, el área o superficie de un triángulo se calcula con la siguiente fórmula:

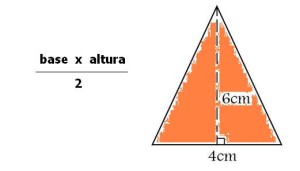En el caso que vemos en la imagen, se observa que la altura es igual a 6 cm y que la base son 4 cm. Por tanto al aplicar la fórmula mencionada, estaríamos multiplicando estas dos medidas lo cual nos daría 24 cm, al dividirlo entre dos, el resultado final son 12 cm cuadrados. Recordemos que en las medidas de superficie, hablamos de cm cuadrados, metros cuadrados etc.

*Tomado de:https://matematicasmodernas.com/triangulos-clasificacion-y-propiedades/

triángulos congruentes

Son aquellas figuras cuyos angulos correspondientes son proporcionales , asi los triángulos semejantes tienen la misma forma pero no necesariamente la misma magnitud.

SE DENOTAN CON ESTOS SÍMBOLOS:

EJERCICIO:

POSTULADOS DE CONGRUENCIA

PARA DETERMINAR SI UN TRIANGULO ES CONGRUENTE NO ES NECESARIO COMPARAR TODOS SUS ELEMENTOS EXISTEN POSTULADOS LOS CUALES NOS PERMITEN COMPARAR

Triángulo	Postulados de congruencia
	Postulado LAL (Lado, Ángulo, Lado) Dos triángulos son congruentes si dos lados de uno tienen la misma longitud que los dos lados del otro triángulo, y los ángulos comprendidos entre esos lados tienen también la misma medida.
	Postulado ALA (Ángulo, Lado, Ángulo) Dos triángulos son congruentes si dos ángulos interiores y el lado comprendido entre ellos tienen la misma medida y longitud, respectivamente. (El lado comprendido entre dos ángulos es el lado común a ellos).
	Postulado LLL (Lado, Lado, Lado) Dos triángulos son congruentes si cada lado de un triángulo tiene la misma longitud que los correspondientes del otro triángulo.